# 排序算法
# 介绍
# 什么是排序
排序(sorting)的功能是将一个数据元素的任意序列,重写排列成一个按关键字有序的序列。其确切的定义为:假设有n个数据元素的序列(R1,R2.,。。。,Rn),其相应关键字的序列是(K1,K2,。。。,Kn)。通过排序要求找出下标1,2,。。。,n的一种排列p1,p2,。。。,pn,使得相应关键字满足如下的非递减(或非递增)关系Kp 1<= Kp 2 <=…<= Kp n这样,就得到一个按关键字有序的记录序列:(Rp1,Rp2,。。。,Rpn)
# 内部排序和外部排序
- 一类是整个排序过程在内存储器中进行,称为内部排序;
- 另一类是由于带排序元素数量台打,以至于内存储器无法容纳全部数据,排序需要借助外存储设备才能完成,这类排序称为外部排序。
# 稳定排序和不稳定排序
如果在待排序的序列中存在多个具有相同关键字的元素,假设Ki = Kj(1<=i<=n,1<=j<=n,i != j),若在排序之前的序列中Ri在Rj之前,经过排序后得到的序列中Ri仍然在Rj之前,则称所用的排序方法是稳定的;否则,当相同关键字元素的前后关系在排序中发生编号,则称所用的排序方法是不稳定的。 无论是稳定的还是不稳定的排序方法,均能完成排序的功能。在某些场合可能对排序有稳定性的要求,此时就应当选择稳定的排序方法。例如假设一组学生记录已经按照学号有序,现在需要根据学生的成绩排序,当分数相同时要求学号小的学生在前,显然此时对分数进行排序就必须选择稳定的排序方法。
排序前(56,34,47,23,66,18,82,47) 若排序后得到结果(18,23,34,47,47,56,66,82),则称该排序方法是稳定的 若排序后得到结果(18,23,34,47,47,56,66,82),则称该排序方法是不稳定的
# 比较排序和非比较排序
大部分排序都是需要通过比较来判断大小,作为排序的依据的。但是也有例外的,避暑计数排序、基数排序、不需要进行比较。 插入排序:将无需子列中的一个过几个记录“插入”到有序序列中,从而增加记录的有序子序列的长度 交换排序:通过“交换”无序序列中的记录从而得到其中关键字最小或最大的记录,并将它加入到有序子序列中国,以此方法增加记录的有序子序列长度。 选择排序:从记录的无序子序列中“选择”关键字最小或最大的记录,并将它加入到有序子序列中,以此方法增加记录的有序子序列的长度。 归并排序:通过”归并“两个或两个以上的记录有序子序列,逐步增加记录有序序列的长度
# 排序类型
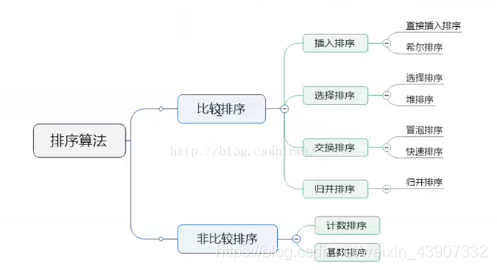
一般说是八大排序类型 另外还可以加上非比较的计数排序、选择排序中的树形选择排序、插入排序中的折半插入排序。
# 排序效率
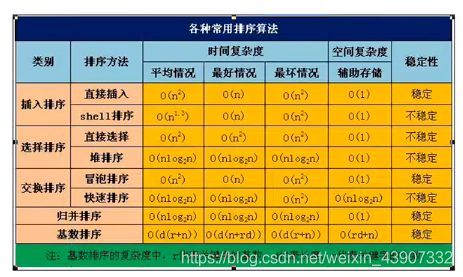
时间复杂度最高的就是三种 基本排序:直接插入、简单选择、冒泡排序。 建议优先掌握直接擦汗如、简单选择、冒泡排序、快速排序
# 冒泡排序
基本思想:重复的走过要排序的数列,一次比较两个元素,相邻两个元素进行交换,直到没有在需要交换为止。
- a)比较相邻的元素。如果第一个比第二个大,就交换他们两个;
- b)对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。在这一点,最后的元素应该会是最大的数;
- c)针对所有的元素重复以上的步骤,除了最后一个;
- d)持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较;
const arr: number[] = [2, 4, 6, 1, 10, 8, 7, 3, 9, 5]
function bubbleSort(array: number[]) {
let temp
let changed = true //降低排序无用次数
for (let i = 0; i < array.length - 1 && changed; i++) {
changed = false
for (let j = 0; j < array.length - i - 1; j++) {
if (array[j] > array[j + 1]) {
temp = array[j]
array[j] = array[j + 1]
array[j + 1] = temp
changed = true
}
}
console.log(array, `======${i}=====`)
}
console.log(array)
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
执行的过程

# 简单选择排序
基本思想:每一次从待排序的数据元素中选出最小(或最大)的一个元素,才放在序列的起始位置,直到全部待排序的数据元素排完为止!
按顺序,从数组arr中,选择一个索引是 i 元素与后边索引是 j 的元素对比,根据条件(较大/较小)更换两个元素位置,一直对比到数组arr到最后,目的选择出最大/最小的元素,并将之更换到 i 的位置。
WARNING
一次可能更改 i 之后的多个元素。
const arr: number[] = [2, 4, 6, 1, 10, 8, 7, 3, 9, 5]
function changeSort(array: number[]) {
let temp
for (let i = 0; i < array.length - 1; i++) {
for (let j = i + 1; j < array.length; j++) {
if (array[i] > array[j]) {
temp = array[i]
array[i] = array[j]
array[j] = temp
}
}
console.log(`选择排序======${i}=====`, array)
}
console.log(`选择排序===result===`, array)
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
执行的过程

# 插入排序
基本思想:每步将一个待排序的记录,按其关键码值的大小插入前面已经排好序的数组中适当位置,直到全部插入为止!
将数组索引是 i 的元素,依次和 i 之前的元素对比,满足条件(较大/较小)就将元素后移一位,直至不需要移动,将 i 元素赋值到该位置。目的是将 i 位置的元素按顺序插入到他之前的某个位置或者它本身位置不变。
WARNING
一次可能更改一个元素的顺序。
const arr: number[] = [2, 4, 6, 1, 10, 8, 7, 3, 9, 5]
function insertSorting(array: number[]) {
let j, temp
for (let i = 1; i < array.length; i++) {
temp = array[i]
for (j = i - 1; j >= 0 && array[j] > temp; j--) {
array[j + 1] = array[j]
}
array[j + 1] = temp
console.log(`插入排序======${i}=====`, array)
}
console.log(`插入排序===result===`, array)
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
执行的过程

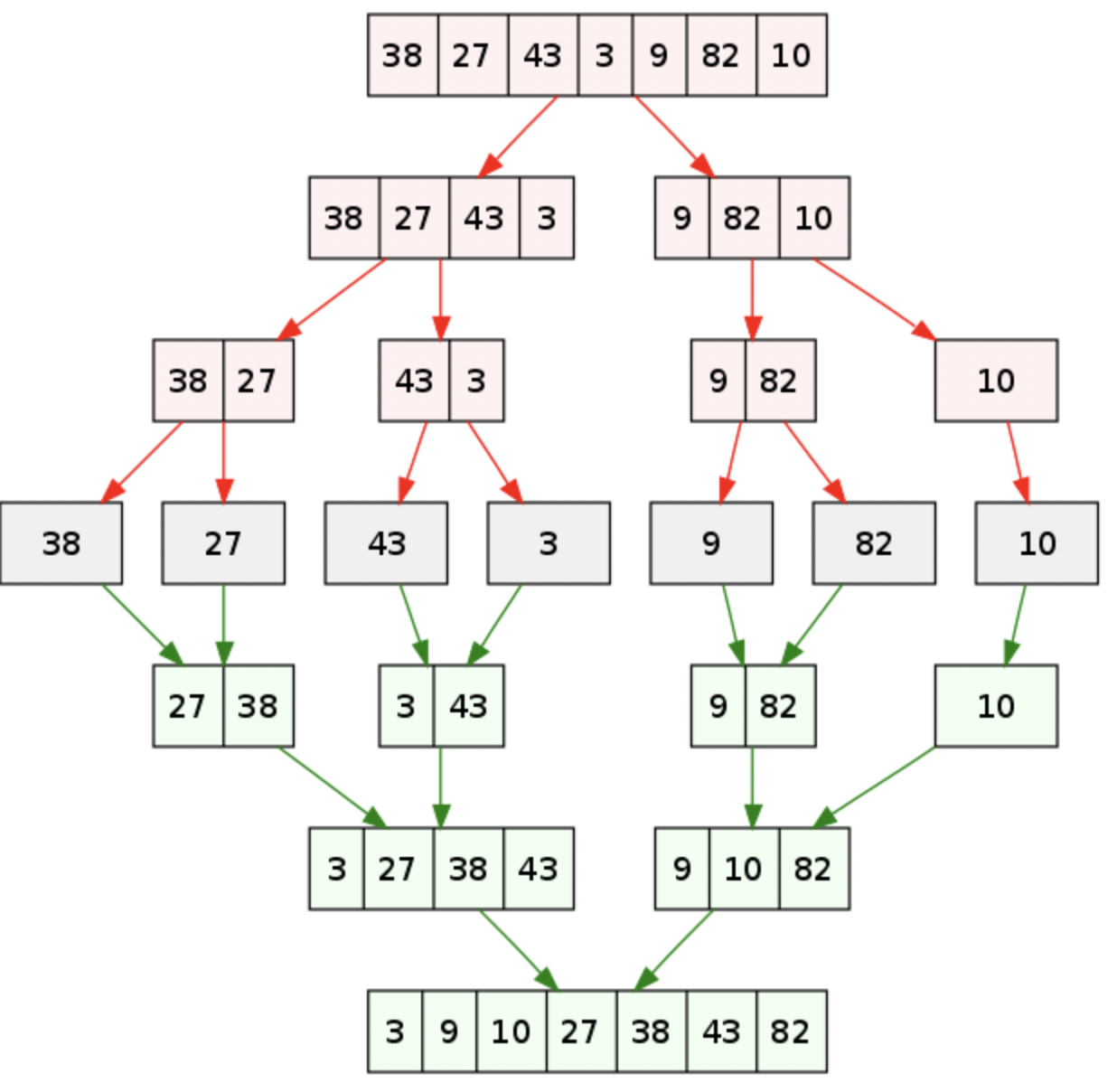
# 二路归并排序
基本思想:采用分治算法来对其一个数组进行划分合并,直到划分的组中只有一个数组元素为止!
首先针对最小单([2, 4])位进行排序,然后再更大的集合([2, 4, 6, 1, 10])里,对两个小集合([2, 4, 6] 和 [1, 10]排序,以此类推,到最后,会对array 前后两部分([2, 4, 6, 1, 10] 和 [8, 7, 3, 9, 5])进行排序。
const arr: number[] = [2, 4, 6, 1, 10, 8, 7, 3, 9, 5]
function mergeSort(array: number[], left: number, right: number) {
if (left == right) {
return
}
let mid = Math.floor((left + right) / 2)
let formatArr: number[] = mergeSort(array, left, mid) //左边递归求解
formatArr = mergeSort(formatArr, mid + 1, right) //右边递归求解
let tempArray = new Array(formatArr.length)
let i = left
let j = mid + 1
let k = left
while (i <= mid || j <= right) {
//当右区间比较完毕,或者左区间的值存在并且比右区间的值小
if (j > right || (i <= mid && formatArr[i] < formatArr[j])) {
tempArray[k++] = formatArr[i++] //将左区间的值放入临时数组中
} else {
tempArray[k++] = formatArr[j++] //右区间的值存在,且比左区间的值小,放入临时数组中
}
}
//将临时数组中的值拷贝到原来数组中
for (k = left; k <= right; k++) {
formatArr[k] = tempArray[k]
}
console.log(`二路归并排序===result===`, formatArr, 'tempArray', tempArray)
return formatArr;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
执行的过程

# 快速排序
基本思想:采用分治算法通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据比另外一部分的所有数据都要小,然后再按此方法对这部分数据进行快速排序,整个排序过程可以递归进行,依此达到整个数据编程有序序列!
- 1、找出基准值索引为 i 的 base;
- 2、倒序查找小于 base等于 的值 min,索引为m,将min赋值到 索引为i的位置,(此时,索引i和m 的值都是min);
- 3、然后正序从索引 i 开始查找 大于 base的值max,索引为x;
- 4、将max赋值给 索引为m的位置;(此时,索引 m 和 x 的值都为 max);
- 5、将base赋值为索引为x的位置,(此时:i: min, x:base,m: max)
- 6、将整个数组分为left到x和x+1 到right两部分,递归。
最终,使每个基准值的左侧使小于等于基准值的,右侧是大于基准值的
const arr: number[] = [5, 4, 6, 2, 1, 10, 7, 3, 8, 9];
function quickSort(array: number[], left: number, right: number) {
// console.log('====', array);
if (left >= right) {
//如果left >= right就说明已经整理完一个组
return array;
}
let i = left;
let j = right;
let temp = array[left]; //找出一个枢纽存储值
while (i < j) {
while (i < j && array[j] >= temp) {
j--;
}
array[i] = array[j];
// console.log(`快速排序=step1=`, array);
while (i < j && array[i] <= temp) {
i++;
}
array[j] = array[i];
}
array[i] = temp;
let formatArr: number[] = quickSort(array, left, i); //左边递归
formatArr = quickSort(array, i + 1, right); //右边递归
console.log(`快速排序===result===`, formatArr);
return formatArr;
}
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
执行的过程
[5, 4, 6, 2, 1, 10, 7, 3, 8, 9];

快速排序是冒泡排序的升级版,最坏情况下每一次基准元素都是数组中最小或者最大的元素,则快速排序就是冒泡排序
这种情况时间复杂度就是冒泡排序的时间复杂度:T[n] = n * (n-1) = n^2 + n,也就是O(n^2)
最好情况下是O(nlogn),其中递归算法的时间复杂度公式:T[n] = aT[n/b] + f(n),推导如下所示。
← 贪心算法 和 回溯算法 数组去重 →